Number of roots of a quadratic equation, $ax^2 + bx + c = 0$
General cases:
1. If equation has two real and distinct roots, then $b^2 - 4ac$ $ > 0 $
2. If equation has two real and equal roots (or one real root), then $b^2 - 4ac$ $ = 0 $
3. If equation has real roots (either one or two real roots), then $b^2 - 4ac$ $ \ge 0 $
4. If equation has no real roots, then $b^2 - 4ac$ $ < 0 $
y = ax2 + bx + c is always positive or always negative
$y = ax^2 + bx + c$ is always positive:
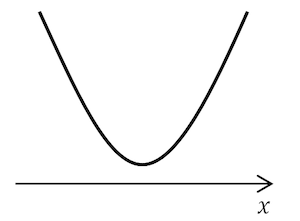
$\text{Condition 1: } $
$ a > 0 $
$\text{Condition 2: } b^2 - 4ac $
$ < 0 $
$y = ax^2 + bx + c$ is always negative:
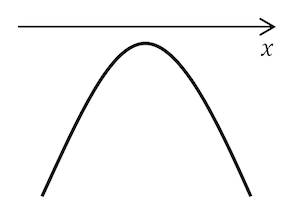
$\text{Condition 1: } $
$ a < 0 $
$\text{Condition 2: } b^2 - 4ac $
$ < 0 $
Questions
Number of roots of a quadratic equation
1. Find the range of values of $k$ such that the equation $(x - 1)^2 = -kx - k$ has real roots.
Answer: $ k \le 0 \text{ or } k \ge 8 $
Solutions
\begin{align}
(x - 1)^2 & = -kx - k \\
x^2 - 2(x)(1) + 1^2 & = -kx - k
\phantom{000000} [(a - b)^2 = a^2 - 2ab + b^2] \\
x^2 - 2x + 1 & = -kx - k \\
x^2 + kx - 2x + 1 + k & = 0 \\
x^2 + (k - 2)x + (1 + k) & = 0 \\
\\
b^2 - 4ac & = (k - 2)^2 - 4(1)(1 + k) \\
& = k^2 - 2(k)(2) + 2^2 - 4(1 + k) \\
& = k^2 - 4k + 4 - 4 - 4k \\
& = k^2 - 8k \\
\\
b^2 - 4ac & \ge 0
\phantom{000000} [\text{Equation has real roots - 1 or 2}] \\
k^2 - 8k & \ge 0 \\
k(k - 8) & \ge 0
\end{align}

$$ k \le 0 \text{ or } k \ge 8 $$
Always positive or always negative
2. Find the range of values of $k$ for which the curve $y = 3x + 1 - kx^2 - kx $ lies entirely above the $x$-axis.
Answer: $ -6 < k < 0 $
Solutions
\begin{align}
y & = 3x + 1 - kx^2 - kx \\
y & = - kx^2 + 3x - kx + 1 \\
y & = (- k)x^2 + (3 - k)x + 1 \\
\\
- k & > 0
\phantom{000000} [\text{Minimum curve } \cup \text{ so } a > 0]\\
k & < 0
\phantom{000000} [\text{Condition #1}] \\
\\ \\
b^2 - 4ac & = (- k)^2 - 4(3 - k)(1) \\
& = k^2 - 4(3 - k) \\
& = k^2 - 12 + 4k \\
& = k^2 + 4k - 12 \\
& = (k + 6)(k - 2) \\
\\
b^2 - 4ac & < 0
\phantom{000000} [\text{No real roots since curve lies above } x \text{-axis}] \\
(k + 6)(k - 2) & < 0
\end{align}

$$ -6 < k < 2 \phantom{000000} [\text{Condition #2}] $$

$$ -6 < k < 0 $$
3. Find a possible set of values of the constants $a$ and $c$ so that the expression $ax^2 + ax + c$ is always negative.
Solutions
\begin{align}
a & < 0
\phantom{000000} [\text{Condition #1}] \\
\\ \\
b^2 - 4ac & = (a)^2 - 4(a)(c) \\
& = a^2 - 4ac \\
\\
b^2 - 4ac & < 0 \\
a^2 - 4ac & < 0
\phantom{000000} [\text{Condition #2}] \\
\\
\text{Let } & a = -1,
\phantom{000} [\text{to satisfy condition #1}] \\
(-1)^2 - 4(-1)c & < 0 \\
1 + 4c & < 0 \\
4c & < - 1 \\
c & < - {1 \over 4} \\
\\ \\
\therefore a & = -1, c = -1
\end{align}
Show/explanation question
4. The cost in thousands of dollars, $C$, in producing $n$ hundred pairs of a certain type of running shoes is given by the equation $C = 1.2n^2 - 14.4n + 53.7$.
Use the discriminant to show that it is not possible to have a cost of production of $10$ thousand dollars.
(from Additional Maths 360 Ex 1.3)
Solutions
\begin{align}
\text{When } & C = 10, \\
10 & = 1.2n^2 - 14.4n + 53.7 \\
0 & = 1.2n^2 -14.4n + 43.7 \\
\\
[a = 1.2, b & = -14.4, c = 43.7] \\
\\
b^2 - 4ac & = (-14.4)^2 - 4(1.2)(43.7) \\
& = -2.4 < 0 \\
\\
\text{Since } b^2 - 4ac < 0, & \phantom{0} \text{equation has no real solutions}. \\
\\
\therefore \text{It is not possible to have } & \text{a cost of production of 10 thousand dollars.}
\end{align}
5. Show that the equation $ p(x + 1) = 3 - {1 \over 2}x^2$ has two real and distinct roots for all real values of $p$.
Solutions
\begin{align}
p(x + 1) & = 3 - {1 \over 2}x^2 \\
px + p & = 3 - {1 \over 2}x^2 \\
{1 \over 2}x^2 + px + (p - 3) & = 0 \\
\\
b^2 - 4ac & = (p)^2 - 4 \left(1 \over 2\right)(p - 3) \\
& = p^2 - 2(p - 3) \\
& = p^2 - 2p + 6 \\
& = p^2 - 2p + \left(2 \over 2\right)^2 - \left(2 \over 2\right)^2 + 6
\phantom{000000} [\text{Complete the square}] \\
& = (p - 1)^2 - 1 + 6 \\
& = (p - 1)^2 + 5 \\
\\
\text{For all real val} & \text{ues of } p, \\
(p - 1)^2 & \ge 0 \\
(p - 1)^2 + 5 & \ge 5 \\
\\ \\
\therefore \text{For all real values of }p, \phantom{.} & b^2 - 4ac > 0
\text{ and equation has two real and distinct roots}
\end{align}
Past year O level questions
| Year & paper |
Comments |
| 2023 P1 Question 7 |
Quadratic curve lies completely below x-axis |
| Specimen P2 Question 4b |
Quadratic expression is always negative (Open-ended question like question 3) |
| 2020 P2 Question 2b |
Quadratic expression is always negative |
| 2018 P2 Question 9ii |
Quadratic expression cannot be negative |
| 2015 P1 Question 4 |
Quadratic expression is always negative (Open-ended question like question 3) |
| 2011 P2 Question 1i |
Quadratic curve is completely above x-axis |
| 2008 P1 Question 10 |
Quadratic expression is (a) always positive (b) always negative |
← Solve quadratic inequality
Intersection(s) between line and curve →




