Completing the square
Formula (optional to use):
$ x^2 \pm bx + c $ = $ \left(x \pm {b \over 2} \right)^2 - \left(b \over 2\right)^2 + c $
Make sure the coefficient of $x^2$ is equals to $1$ before applying the formula (see part ii and iii below).
Practice
(i) Express $ x^2 + 4x + 5 $ in the form $ a(x - h)^2 + k $.
Answer: $(x + 2)^2 + 1$
Solutions
\begin{align}
x^2 + 4x + 5 & = x^2 + 4x + \left(4 \over 2\right)^2 - \left(4 \over 2\right)^2 + 5 \\
& = x^2 + 4x + 2^2 - 2^2 + 5 \\
& = (x + 2)^2 - 4 + 5 \\
& = (x + 2)^2 + 1
\end{align}
(ii) Express $ {1 \over 4}x^2 - 2x - 10 $ in the form $a(x - h)^2 + k$.
Answer: $ {1 \over 4} (x - 4)^2 - 14$
Solutions
\begin{align}
{1 \over 4}x^2 - 2x - 10 & = {1 \over 4} (x^2 - 8x) - 10
\phantom{0000000} [\text{must be } x^2 \text{ before completing the square}] \\
& = {1 \over 4} \left[ x^2 - 8x + \left(8 \over 2\right)^2 - \left(8 \over 2\right)^2 \right] - 10 \\
& = {1 \over 4} ( x^2 - 8x + 4^2 - 4^2 ) - 10 \\
& = {1 \over 4} [ (x - 4)^2 - 16 ] - 10 \\
& = {1 \over 4} (x - 4)^2 - 4 - 10 \\
& = {1 \over 4} (x - 4)^2 - 14
\end{align}
(iii) Express $ 9 + 3 x - 2x^2 $ in the form $c - a(x - b)^2 $.
Answer: $ {81 \over 8} - 2 \left(x - {3 \over 4}\right)^2 $
Solutions
\begin{align}
9 + 3x - 2x^2 & = - 2x^2 + 3x + 9 \\
& = -2 \left(x^2 - {3 \over 2}x \right) + 9 \\
& = -2 \left[ x^2 - {3 \over 2}x + \left(3 \over 4\right)^2 - \left(3 \over 4\right)^2 \right] + 9 \\
& = -2 \left[ \left(x - {3 \over 4}\right)^2 - {9 \over 16} \right] + 9 \\
& = -2 \left(x - {3 \over 4}\right)^2 + {9 \over 8} + 9 \\
& = -2 \left(x - {3 \over 4}\right)^2 + {81 \over 8} \\
& = {81 \over 8} - 2 \left(x - {3 \over 4}\right)^2
\end{align}
Maximum value or minimum value of $ a(x - h)^2 + k $
Deducing maximum value or minimum value:
$$ a(x - h)^2 + k $$
$ \text{If } a > 0, \text{ expression has minimum value of } k \text{ when } x = h $
$ \text{If } a < 0, \text{ expression has maximum value of } k \text{ when } x = h $
Practice
(i) For $ - 2(x + 3)^2 + 10$,
- Maximum value of $ 10 $ when $x = $ $ -3 $
- The graph of $y = - 2(x + 3)^2 + 10$ is a maximum $ (\cap) $ curve with turning point $ (-3, 10)$
(ii) For $ 3(x - 4)^2 - 5 $,
- Minimum value of $ -5 $ when $x = $ $ 4 $
- The graph of $y = 3(x - 4)^2 - 5$ is a minimum $ (\cup) $ curve with turning point $ (4, -5)$
Questions
Sketch graph
To sketch the graph in this form, we need to know:
- Shape ($ \cap $ or $ \cup $)
- Coordinates of turning point
- $y$-intercept (Let $x = 0$)
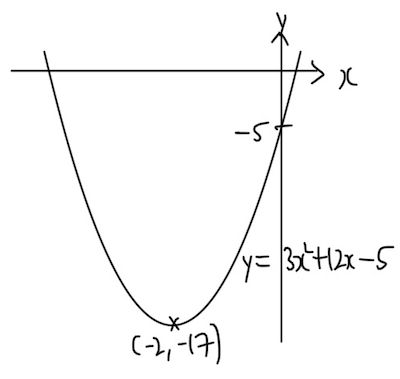
Q1. By first expressing $3x^2 + 12x - 5$ in the form $a(x - h)^2 + k$, sketch the graph of $y = 3x^2 + 12x - 5$. Show clearly the coordinates of the turning point and the $y$-intercept.
(from think! Workbook A Review Ex 1)
Answer: $ 3(x + 2)^2 - 17 $
Solutions
\begin{align}
3x^2 + 12x - 5 & = 3(x^2 + 4x) - 5 \\
& = 3 \left[ x^2 + 4x + \left(4 \over 2\right)^2 - \left(4 \over 2\right)^2 \right] - 5 \\
& = 3 (x^2 + 4x + 2^2 - 2^2 ) - 5 \\
& = 3 [(x + 2)^2 - 4] - 5 \\
& = 3(x + 2)^2 - 12 - 5 \\
& = 3(x + 2)^2 - 17 \\
\\
y & = 3x^2 + 12x - 5
\phantom{0000000} [\text{Minimum curve } \cup] \\
y & = 3(x + 2)^2 - 17 \\
\\
\text{Turning} & \text{ point: } (-2, -17) \\
\\
\text{Let } & x = 0, \\
y & = 3(0 + 2)^2 - 17 \\
& = -5
\phantom{00000000000000000} [y \text{-intercept}]
\end{align}
Explanation/show question
Q2. Explain why the expression $-3x^2 + 6x - 8$ is always negative for all real values of $x$.
Solutions
\begin{align}
-3x^2 + 6x - 8 & = -3 (x^2 - 2x) - 8 \\
& = -3 \left[ x^2 - 2x + \left(2 \over 2\right)^2 - \left(2 \over 2\right)^2 \right] - 8 \\
& = -3 (x^2 - 2x + 1^2 - 1^2) - 8 \\
& = -3 [ (x - 1)^2 - 1] - 8 \\
& = -3 (x - 1)^2 + 3 - 8 \\
& = -3(x - 1)^2 - 5 \\
\\
\text{For all real } & \text{values of } x, \\
(x - 1)^2 & \ge 0 \\
-3(x - 1)^2 & \le 0 \\
-3(x - 1)^2 -5 & \le -5 \\
\\
\therefore \text{Expression is always} & \text{ negative for all real values of } x
\end{align}
Q3. Explain why the graph of $y = 2x^2 - 4x + 3$ lies entirely above the $x$-axis.
Solutions
\begin{align}
y & = 2x^2 - 4x + 3 \\
& = 2(x^2 - 2x) + 3 \\
& = 2 \left[ \left(x - {2 \over 2}\right)^2 - \left(2 \over 2\right)^2 \right] + 3 \\
& = 2 [ (x - 1)^2 - 1 ] + 3 \\
& = 2(x - 1)^2 -2 + 3 \\
& = 2(x - 1)^2 + 1 \\
\\
\text{Minimum} & \text{ curve } (\cup) \text{ with turning point } (1, 1)
\end{align}
$$ \text{Since the minimum point of the graph lies above the } x \text{-axis, the entire curve lies above the } x \text{-axis}$$
Open-ended question (i.e. many possible answers accepted)
Q4. The graph of $y = ax^2 + 2x + c$, where $a$ and $c$ are integers, lies entirely below the $x$-axis. Suggest a possible set of values of $a$ and $c$.
Solutions
\begin{align}
y & = ax^2 + 2x + c \\
\\
\text{For curve to lie } & \text{below } x \text{-axis, curve must be a maximum curve } (\cap) \\
\\
\implies & \text{Condition #1: } a < 0 \\
\\ \\
y & = ax^2 + 2x + c \\
& = a \left(x^2 + {2 \over a}x\right) + c \\
& = a \left[ x^2 + {2 \over a}x + \left(1 \over a\right)^2 - \left(1 \over a\right)^2 \right] + c \\
& = a \left[ \left(x + {1 \over a}\right)^2 - {1 \over a^2} \right] + c \\
& = a \left(x + {1 \over a}\right)^2 - {a \over a^2} + c \\
& = a \left(x + {1 \over a}\right)^2 - {1 \over a} + c \\
\\
\text{Turning point: } & \left(-{1 \over a}, -{1 \over a} + c \right)
\phantom{000000} [\text{Must be below } x \text{-axis}] \\
\\
-{1 \over a} + c & < 0 \\
\text{Condition #2: } c & < {1 \over a} \\
\\ \\
\text{Let } & a = -1,
\phantom{000000} [\text{to satisfy condition #1}] \\
c & < {1 \over -1} \\
c & < -1 \\
\\ \\
\text{Possible values: } & a = -1, c = -2
\end{align}
Real-life problem
Q5. The cost, \$ $y$, of assembling $x$ model helicopters can be approximated by $y = {5 \over 4}x^2 - 20x + 340$, where $x \le 10$.
(from think! Workbook A Worksheet 1B)
(i) Find the value of $y$ when $x = 0$. State what you think the value of $y$ represents.
Answer: $ y = 340 $
Solutions
\begin{align*}
y & = {5 \over 4}x^2 - 20x + 340 \\
\\
\text{When } & x = 0, \\
y & = {5 \over 4}(0)^2 - 20(0) + 340 \\
& = 340 \\
\\
340 \text{ is } & \text{the fixed cost of assembly}
\end{align*}
(ii) The manager wants to reduce the cost to \$ 250. Show how you would convince him that it is not possible.
Solutions
\begin{align*}
y & = {5 \over 4}x^2 - 20x + 340 \\
& = {5 \over 4}(x^2 - 16x) + 340 \\
& = {5 \over 4} \left[ x^2 - 16x + \left(16 \over 2\right)^2 - \left(16 \over 2\right)^2 \right] + 340 \\
& = {5 \over 4} ( x^2 - 16x + 8^2 - 8^2 ) + 340 \\
& = {5 \over 4} [ (x - 8)^2 - 64 ] + 340 \\
& = {5 \over 4} (x - 8)^2 - 80 +34 0\\
& = {5 \over 4} (x - 8)^2 + 260 \\
\\
\text{Minimum cost } (y) & = 260 \text{ when } x = 8 \\
\\
\therefore \text{Not possible } & \text{for cost to be } \$ 250
\end{align*}
Past year O level questions (first introduced in 2021)
| Year & paper |
Comments |
| 2024 P1 Question 9a |
Part a: Roots of equation
Part b: Form equation of curve |
| 2023 P1 Question 12 |
Real-life problem |
| 2022 P1 Question 1a |
Complete the square and deduce turning point of graph |
| 2021 P1 Question 3 |
Complete the square and deduce turning point of graph |
| Specimen P1 Question 7 |
Part a: Complete the square
Part b: Explain why quadratic curves don't intersect |
Equation & inequalities: Solve quadratic inequality →
(Subscription required)