Formulas
Distance between two points $A(x_1, y_1)$ and $B (x_2, y_2)$:
$ AB $ = $ \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $
Gradient of line passing through two points $A(x_1, y_1)$ and $B (x_2, y_2)$:
$ \text{Gradient of } AB $ = $ {y_2 - y_1 \over x_2 - x_1} $
Midpoint of two points $A(x_1, y_1)$ and $B (x_2, y_2)$:
$ \text{Midpoint of } AB $ = $ \left( {x_1 + x_2 \over 2}, {y_1 + y_2 \over 2} \right) $
Working backwards from midpoint
Example
Given that the point $M(2.5, 2.5)$ is the midpoint of the points $C(1, 4)$ and $D$, find the coordinates of point $D$.
Answer: $ D(4, 1) $
Solutions

\begin{align*}
\text{Let coordinates} & \text{ of } D \text{ be } (a, b) \\
\\
\text{Mid-point of } CD & \text{ is } \left({1 + a \over 2}, {4 + b \over 2}\right) \\
\\
\text{Comparing } & \text{with } M(2.5, 2.5),
\end{align*}
\begin{align*}
{1 + a \over 2} & = 2.5 &&& {4 + b \over 2} & = 2.5 \\
1 + a & = 2(2.5) &&& 4 + b & = 2(2.5) \\
1 + a & = 5 &&& 4 + b & = 5 \\
a & = 5 - 1 &&& b & = 5 - 4 \\
a & = 4 &&& b & = 1
\end{align*}
$$ \therefore D(4, 1) $$
Equation of straight line
Equation of a non-vertical straight line:
$ \text{Equation: } $$ y = mx + c $
$ m \text{ represents the } $$ \text{gradient of the straight line} $
$ c \text{ represents the } $$ y\text{-intercept of the straight line} $
Equation of a horizontal line:
$ \text{Equation of horizontal line passing though } (a, b) \text{:} $$ \phantom{.} y = b $
$ \text{Gradient of line} $ = $ \phantom{0} 0 \phantom{0} $
Equation of a vertical line:
$ \text{Equation of vertical line passing though } (a, b) \text{:} $$ \phantom{.} x = a $
$ \text{Gradient of line is} $ $ \text{ undefined } $
Example
The diagram below shows two points, $A(2, 3)$ and $B(1, 1)$.

(i) State the equation of the horizontal line $l_1$.
Answer: $ y = 3 $
(ii) State the equation of the vertical line $l_2$.
Answer: $ x = 2 $
(iii) Form the equation of the straight line that passes through points $A$ and $B$.
Answer: $ y = 2x - 1 $
Solutions
\begin{align*}
m & = {3 - 1 \over 2 - 1} \\
& = 2 \\
\\
y & = mx + c \\
y & = 2x + c \\
\\
\text{Using } & B(1, 1), \\
1 & = 2(1) + c \\
1 & = 2 + c \\
-1 & = c \\
\\
\text{Eqn of line: } & y = 2x - 1
\end{align*}
Find angle between line and axes
Example
Line $l$ has gradient of $-2$ and $y$-intercept $2$.
(i) Find the acute angle between line $l$ and the $y$-axis.
Answer: $ 26.6^\circ $
Solutions
\begin{align*}
y & = mx + c \\
y & = -2x + 2 \\
\\
\text{Let } & y = 0, \\
0 & = -2x + 2 \\
2x & = 2 \\
x & = 1 \phantom{000000} [x \text{-intercept}]
\end{align*}

\begin{align*}
\tan \theta & = {1 \over 2} \phantom{000000} \left[ {Opp \over Adj} \right] \\
\theta & = \tan^{-1} \left(1 \over 2\right) \\
\theta & = 26.565^\circ \\
\theta & \approx 26.6^\circ
\end{align*}
(ii) Find the obtuse angle between line $l$ and the $x$-axis.
Answer: $ 116.6^\circ $
Solutions

\begin{align*}
\tan \alpha & = {2 \over 1} \phantom{000000} \left[ {Opp \over Adj} \right] \\
\alpha & = \tan^{-1} \left(2 \over 1\right) \\
\alpha & = 63.435^\circ \\
\\
\text{Obtuse angle} & = 180^\circ - 63.435^\circ \\
& = 116.565^\circ \\
& \approx 116.6^\circ
\end{align*}
Collinear points
Collinear points
If two or more points are collinear, then they lie on the same straight line. Thus,
- Gradient between any two points is the same
- The coordinate of each point must satisfy the equation of the straight line
Example: Prove that points are collinear
Prove that the points $E(1, 2)$, $F(2.5, 3)$ and $G(4, 4)$ are collinear.
Solutions (by finding gradient)

\begin{align*}
\text{Gradient of } EF & = {3 - 2 \over 2.5 - 1} \\
& = {2 \over 3} \\
\\
\text{Gradient of } FG & = {4 - 3 \over 4 - 2.5} \\
& = {2 \over 3} \\
\\
\therefore E, F \text{ and } G & \text{ lie on the same line}
\end{align*}
Solutions (by equation of line)

\begin{align*}
\text{Gradient of } EF & = {3 - 2 \over 2.5 - 1} \\
& = {2 \over 3} \\
\\
y & = mx + c \\
y & = {2 \over 3}x + c \\
\\
\text{Using } & E(1, 2), \\
2 & = {2 \over 3}(1) + c \\
2 & = {2 \over 3} + c \\
{4 \over 3} & = c \\
\\
\text{Eqn of } EF: & \phantom{0} y = {2 \over 3}x + {4 \over 3} \\
\\
\text{Let } & x = 4, \\
y & = {2 \over 3}(4) + {4 \over 3} \\
y & = 4 \\
\\
\therefore G(4, 4) \text{ lies on line } & \text{passing through } E \text{ and } F
\end{align*}
Example: Find the coordinates of collinear point

The points $A$ and $B$ have coordinates $(-2, 1)$ and $(0, 2)$ respectively. The line $AB$ is produced to point $C$, such that $AB:AC = 1:3$. Find the coordinates of point $C$.
Answer: $ (4, 4) $
Solutions (by column vectors)

\begin{align*}
\underbrace{ \overrightarrow{AB} }_{\text{Moving from } A \text{ to } B}
& = {2 \choose 1}
\phantom{000000} [2 \text{ units in }x \text{-direction, } 1 \text{ unit in } y \text{-direction}] \\
\\
\overrightarrow{AC} & = 3 \overrightarrow{AB} \\
& = 3 {2 \choose 1} \\
& = {6 \choose 3} \\
\\
x \text{-coordinate of } C & = -2 + 6 = 4 \\
\\
y \text{-coordinate of } C & = 1 + 3 = 4 \\
\\
\therefore & \phantom{.} C(4, 4)
\end{align*}
Solutions (by similar triangles)


\begin{align*}
x \text{-coordinate of } C & = -2 + 6 = 4 \\
\\
y \text{-coordinate of } C & = 1 + 3 = 4 \\
\\
\therefore & \phantom{.} C(4, 4)
\end{align*}
Relationship between two lines
Parallel lines:

- If two lines are parallel, they have the same gradient, i.e. $m_1 = m_2$
- If two lines are parallel and do not have the same $y$-intercept, they will not intersect
Non-parallel lines:

Since the lines are not parallel, the lines will meet at a point. The coordinates of the point of intersection can be found by solving simultaneous equations using the equation of each line.
Perpendicular lines:

The gradients of both lines are related by, $m_1 \times m_2 = $ $ - 1 $
Example
(i) Form the equation of the straight line that is parallel to the line $2y - 3x = 5$ and passes through the point $(3, 3)$.
Answer: $ y = {3 \over 2}x - {3 \over 2} $
Solutions
\begin{align*}
2y - 3x & = 5 \\
2y & = 3x + 5 \\
y & = {1 \over 2}(3x + 5) \\
y & = {3 \over 2}x + {5 \over 2} \phantom{000000} [y = mx + c] \\
\\
\text{Gradient of new line} & = {3 \over 2} \phantom{000000000000} [m_1 = m_2] \\
\\
y & = {3 \over 2}x + c \\
\\
\text{Using } & (3, 3), \\
3 & = {3 \over 2}(3) + c \\
3 & = {9 \over 2} + c \\
-{3 \over 2} & = c \\
\\
\text{Eqn of line: } & y = {3 \over 2}x - {3 \over 2}
\end{align*}
(ii) Form the equation of the straight line that is perpendicular to the line $2y - 3x = 5$ and passes through the point $(3, 3)$.
Answer: $ y = -{2 \over 3}x + 5 $
Solutions
\begin{align*}
2y - 3x & = 5 \\
2y & = 3x + 5 \\
y & = {1 \over 2}(3x + 5) \\
y & = {3 \over 2}x + {5 \over 2} \phantom{000000} [y = mx + c] \\
\\
\text{Gradient of new line} & = -1 \div {3 \over 2} \phantom{0000000} [m_1\times m_2 = -1 \implies m_2 = -1 \div m_1] \\
& = -{2 \over 3} \\
\\
y & = -{2 \over 3}x + c \\
\\
\text{Using } & (3, 3), \\
3 & = -{2 \over 3}(3) + c \\
3 & = -2 + c \\
5 & = c \\
\\
\text{Eqn of line: } & y = -{2 \over 3}x + 5
\end{align*}
Form equation of perpendicular bisector
Example
The points $A$ and $B$ have coordinates $(1, 4)$ and $(5, 2)$ respectively. Find the equation of the perpendicular bisector of line segment $AB$.
Answer: $ y = 2x - 3 $
Solutions

\begin{align*}
\left( {1 + 5 \over 2}, {4 + 2 \over 2} \right) & = (3, 3) \\
\\
\text{Mid-point of } AB & \phantom{.} (3, 3) \\
\\
\text{Gradient of } AB & = {4 - 2 \over 1 - 5} \\
& = -{1 \over 2} \\
\\
m_1 \times m_2 & = - 1 \\
\text{Gradient of perpendicular bisector} \times -{1 \over 2} & = -1 \\
\text{Gradient of perpendicular bisector} & = {-1 \over -{1 \over 2}} \\
& = 2 \\
\\
y & = mx + c \\
y & = 2x + c \\
\\
\text{Using midpoint } (3, 3), & \text{ let } x = 3 \text{ and } y = 3, \\
3 & = 2(3) + c \\
3 & = 6 + c \\
3 - 6 & = c \\
-3 & = c \\
\\
\therefore \text{Equation of perpendicular bisector: } & y = 2x - 3
\end{align*}
Find area by 'shoelace' method
Formula & steps:
$ \text{Area of figure} $ = $ {1 \over 2} \left| \begin{matrix} x_1 & x_2 & ... & x_n & x_1 \\ y_1 & y_2 & ... & y_n & y_1 \end{matrix} \right| $
Steps:
- Select the points in anti-clockwise order
- Repeat the first point chosen
- When calculating the area, go ↘ , then go ↗
Example
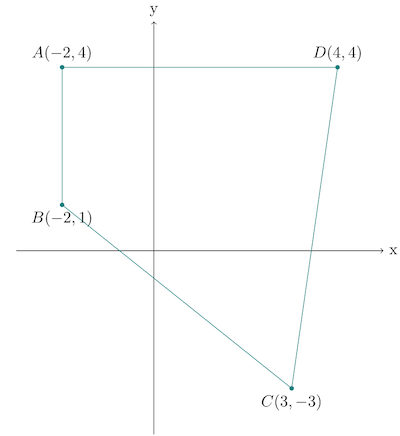
Find the area of the quadrilateral $ABCD$.
Answer: $ 28.5 \text{ units}^2 $
Solutions
\begin{align*}
\text{Area of quadrilateral } ABCD & = {1 \over 2} \left| \begin{matrix} -2 & -2 & 3 & 4 & -2 \\ 4 & 1 & -3 & 4 & 4 \end{matrix} \right| \\
& = {1 \over 2} [ (-2)(1) + (-2)(-3) + (3)(4) + (4)(4) ] - {1 \over 2} [ (4)(-2) + (1)(3) + (-3)(4) + (4)(-2)] \\
& = 28.5 \text{ units}^2
\end{align*}
Past year O level questions
| Year & paper |
Comments |
| 2023 P1 Question 13 |
Perpendicular bisector |
| 4049 Specimen P1 Question 1 |
Find the values of constants a and b (involves y = mx + c and distance between two points) |
| 2013 P1 Question 10 |
Long question |
| 2006 P2 Question 12 Or |
Long question (Link - Subscription required) |
| 2004 P1 Question 11 |
Long question (Link - Subscription required) |
← Logarithms
Coordinate geometry: Geometry problems →












