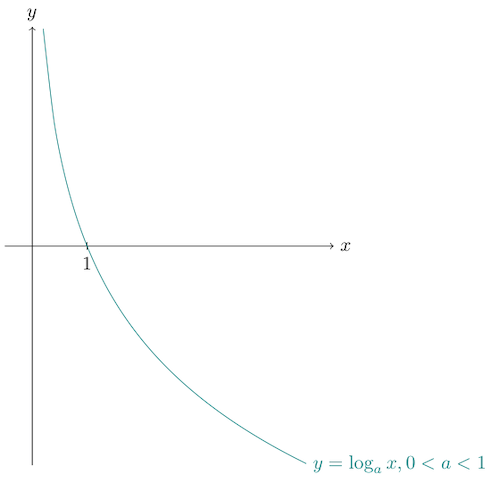
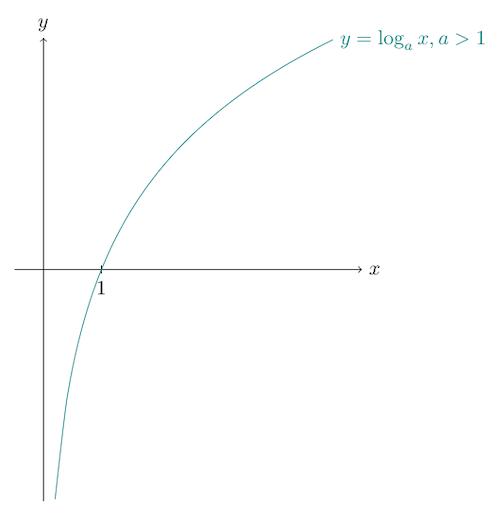Questions
Simplify logarithms
1. Show that
(from A Maths 360 2nd edition Ex 5.3)
(i) $2 \log_a 2 + \log_a 10 - 3 \log_a 3 - \log_a 5 = 3 \log_a {2 \over 3} $
Solutions
\begin{align}
\text{L.H.S} & = 2\log_a 2 + \log_a 10 - 3\log_a 3 - \log_a 5 \\
& = \log_a 2^2 + \log_a 10 - \log_a 3^3 - \log_a 5 \phantom{00000} [\text{Power law}] \\
& = \log_a 4 + \log_a 10 - \log_a 27 - \log_a 5 \\
& = \log_a (4 \times 10) - \log_a 27 - \log_a 5 \phantom{0000000} [\text{Product law}] \\
& = \log_a 40 - \log_a 27 - \log_a 5 \\
& = \log_a {40 \over 27} - \log_a 5 \phantom{000000000000000000} [\text{Quotient law}] \\
& = \log_a { {40 \over 27} \over 5} \\
& = \log_a {8 \over 27} \\
& = \log_a \left(2 \over 3\right)^3 \\
& = 3 \log_a {2 \over 3} \phantom{0} \\
& = \text{R.H.S}
\end{align}
(ii) $ \log_2 27 \times \log_3 25 \times \log_5 16 = 24$
Solutions
\begin{align}
\require{cancel}
\text{L.H.S} & = \log_2 27 \times \log_3 25 \times \log_5 16 \\
& = \log_2 27 \times {\log_2 25 \over \log_2 3} \times {\log_2 16 \over \log_2 5} \phantom{00000} [\text{Change-of-base}] \\
& = {\log_2 27 \times \log_2 25 \times \log_2 16 \over \log_2 3 \times \log_2 5} \\
& = {\log_2 3^3 \times \log_2 5^2 \times \log_2 2^4 \over \log_2 3 \times \log_2 5} \\
& = {3 \cancel{\log_2 3} \times 2 \cancel{\log_2 5} \times 4 \log_2 2 \over \cancel{\log_2 3} \times \cancel{\log_2 5} } \phantom{00000} [\text{Power law}] \\
& = 3 \times 2 \times 4 \log_2 2 \\
& = 6 \times 4(1) \\
& = 24 \\
& = \text{R.H.S}
\end{align}
2. Given that $\log_9 x = p$, express each of the following in terms of $p$.
(from think! A Maths Workbook A Worksheet 6C)
(i) $ \log_9 81x^3$
Answer: $ 2 + 3p $
Solutions
\begin{align}
\log_9 81x^3 & = \log_9 81 + \log_9 x^3
\phantom{000000} [\text{Product law}] \\
& = \log_9 9^2 + \log_9 x^3 \\
& = 2 \log_9 9 + 3 \log_9 x
\phantom{000000} [\text{Power law}] \\
& = 2(1) + 3p \\
& = 2 + 3p
\end{align}
(ii) $ (\log_3 \sqrt{3x})^2 $
Answer: $ {1 \over 4}(1 + 2p)^2 $
Solutions
\begin{align}
(\log_3 \sqrt{3x})^2
& = [ \log_3 (3x)^{1 \over 2} ]^2 \\
& = \left[ {1 \over 2} \log_3 (3x) \right]^2
\phantom{000000000} [\text{Power law}] \\
& = \left[ {1 \over 2} (\log_3 3 + \log_3 x) \right]^2
\phantom{000} [\text{Product law}] \\
& = \left[ {1 \over 2} (1 + \log_3 x) \right]^2
\phantom{000000} [\text{Need to find value of } \log_3 x]\\
\\ \\
\log_9 x & = p \\
{\log_3 x \over \log_3 9} & = p
\phantom{000000} [\text{Change-of-base}] \\
{\log_3 x \over \log_3 3^2} & = p \\
{\log_3 x \over 2 \log_3 3} & = p \\
{\log_3 x \over 2(1)} & = p \\
{\log_3 x \over 2} & = p \\
\log_3 x & = 2p \\
\\ \\
\therefore (\log_3 \sqrt{3x})^2 & = \left[{1 \over 2}(1 + 2p)\right]^2 \\
& = \left(1 \over 2\right)^2 (1 + 2p)^2 \\
& = {1 \over 4}(1 + 2p)^2
\end{align}
Solve logarithmic equation
3. Solve the following equations:
(from think! A Maths Workbook Worksheet 6D)
(i) $ \log_4 (\log_3 x) = 1 $
Answer: $ 81 $
Solutions
\begin{align}
\log_4 (\log_3 x) & = 1 \\
\log_3 x & = 4^1
\phantom{00000} [\text{Change to exponential form}] \\
\log_3 x & = 4 \\
x & = 3^4
\phantom{00000} [\text{Change to exponential form}] \\
x & = 81
\end{align}
(ii) $ \log_4 (x + 10) - \log_4 (x - 2) = \log_4 (x + 3) $
Answer: $ 4 $
Solutions
\begin{align}
\log_4 (x + 10) - \log_4 (x - 2) & = \log_4 (x + 3) \\
\log_4 {x + 10 \over x - 2} & = \log_4 (x + 3)
\phantom{000000} [\text{Quotient law}] \\
\\
{x + 10 \over x - 2} & = x + 3 \\
x + 10 & = (x - 2)(x + 3) \\
x + 10 & = x^2 + 3x - 2x - 6 \\
x + 10 & = x^2 + x - 6 \\
16 & = x^2 \\
\pm \sqrt{16} & = x
\end{align}
\begin{align}
x & = 4 && \text{ or } & x & = -4 \text{ (Reject, since } \log_4 -6 \text{ is undefined})
\end{align}
(iii) $ (\log_2 x)^2 = 9$
Hint: Power law cannot be used since $ (\log_2 x)^2 \ne 2 \log_2 x$. Only $ \log_2 x^2 = 2 \log_2 x$ .
Answer: $ 8 \text{ or } {1 \over 8} $
Solutions
\begin{align}
(\log_2 x)^2 & = 9 \\
\log_2 x & = \pm \sqrt{9} \\
\log_2 x & = \pm 3
\end{align}
\begin{align}
\log_2 x & = 3 && \text{ or } & \log_2 x & = -3 \\
x & = 2^3 &&& x & = 2^{-3} \phantom{00000} [\text{Change to exponential form}] \\
x & = 8 &&& x & = {1 \over 8}
\end{align}
Equation with logarithms of different bases
4. Solve the equation $ \log_4 x^2 + \log_{16} x = \log_3 27 $
Answer: $ 5.28 $
Solutions
\begin{align}
\log_4 x^2 + \log_{16} x & = \log_3 27 \\
\log_4 x^2 + \log_{16} x & = \log_3 3^3 \\
2 \log_4 x + \log_{16} x & = 3 \log_3 3
\phantom{000000} [\text{Power law}] \\
2 \log_4 x + \log_{16} x & = 3(1) \\
2 \log_4 x + {\log_4 x \over \log_4 16} & = 3
\phantom{000000} [\text{Change-of-base}] \\
2 \log_4 x + {\log_4 x \over \log_4 4^2} & = 3 \\
2 \log_4 x + {\log_4 x \over 2 \log_4 4} & = 3 \\
2 \log_4 x + {\log_4 x \over 2 (1)} & = 3 \\
2 \log_4 x + {\log_4 x \over 2} & = 3 \\
2 \left( 2 \log_4 x + {\log_4 x \over 2} \right) & = 2(3) \\
4 \log_4 x + \log_4 x & = 6 \\
5 \log_4 x & = 6 \\
\log_4 x & = {6 \over 5} \\
x & = 4^{6 \over 5}
\phantom{000000} [\text{Change to exponential form}] \\
x & = 5.2780 \\
x & \approx 5.28
\end{align}
Solve logarithmic equation by substitution
5. Solve the equation$ \log_x 4 - 3 \log_2 x = 5 $
Answer: $ {1 \over 4} \text{ or } 1.26 $
Solutions
\begin{align}
\log_x 4 - 3 \log_2 x & = 5 \\
\log_x 4 - 3 \left( \log_x x \over \log_x 2 \right) & = 5
\phantom{0000000} [\text{Change-of-base}] \\
\log_x 4 - 3 \left(1 \over \log_x 2\right) & = 5 \\
\log_x 2^2 - {3 \over \log_x 2} & = 5 \\
2 \log_x 2 - {3 \over \log_x 2} & = 5
\phantom{0000000} [\text{Power law}] \\
\\
\text{Let } u = \log_x 2, & \\
2u - {3 \over u} & = 5 \\
u \left(2u - {3 \over u}\right) & = 5u \\
2u^2 - 3 & = 5u \\
2u^2 - 5u - 3 & = 0 \\
(u - 3)(2u + 1) & = 0
\end{align}
\begin{align}
u - 3 & = 0 && \text{ or } & 2u + 1 & =0 \\
u & = 3 &&& 2u & = -1 \\
& &&& u & = -{1 \over 2} \\
\\
\log_x 2 & = 3 &&& \log_x 2 & = -{1 \over 2} \\
2 & = x^3 &&& 2 & = x^{-{1 \over 2}}
\phantom{000000} [\text{Exponential form}] \\
\sqrt[3]{2} & = x &&& 2 & = {1 \over \sqrt{x}} \\
1.26 & \approx x
&&& 2 \sqrt{x} & = 1 \\
& &&& \sqrt{x} & = {1 \over 2} \\
& &&& x & = \left(1 \over 2\right)^2 \\
& &&& x & = {1 \over 4}
\end{align}
Solve simultaneous equations
6. Solve the simultaneous equations
$$ \ln (3x - y) = \ln 36 - \ln 9 \text{ and } {(e^x)^2 \over e^y} = e $$
(from A Maths 360 2nd edition Ex 5.4)
Answer: $ x = 3, y = 5 $
Solutions
\begin{align}
\ln (3x - y) & = \ln 36 - \ln 9 \\
\ln (3x - y) & = \ln {36 \over 9} \phantom{00000000} [\text{Quotient law}] \\
\ln (3x - y) & = \ln 4 \\
\\
\therefore 3x - y & = 4 \\
- y & = 4 - 3x \\
y & = -4 + 3x \phantom{0} \text{ --- (1)} \\
\\ \\
{(e^x)^2 \over e^y} & = e \\
(e^x)^2 & = e(e^y) \\
[ (a^m)^n = a^{mn}] \phantom{00000000} e^{2x} & = e(e^y) \\
e^{2x} & = e^1 (e^y) \\
e^{2x} & = e^{1 + y} \phantom{00000000} [ (a^m)(a^n) = a^{m + n} ] \\
\\
\therefore 2x & = 1 + y \phantom{000} \text{ --- (2)} \\
\\
\text{Substitute } & \text{(1) into (2),} \\
2x & = (-4 + 3x) + 1 \\
2x & = - 4 + 3x + 1 \\
2x - 3x & = -4 + 1 \\
- x & = -3 \\
x & = 3 \\
\\
\text{Substitute } & x = 3 \text{ into (1),} \\
y & = -4 + 3(3) \\
& = 5 \\
\\ \\
\therefore x & = 3, y = 5
\end{align}
Change subject of equation
7. For the equation $\ln (2x + y) - 3x = 1$, express $y$ in terms of $x$.
Answer: $ y = e^{3x + 1} - 2x $
Solutions
\begin{align}
\ln (2x + y) - 3x & = 1 \\
\ln (2x + y) & = 3x + 1 \\
\log_e (2x + y) & = 3x + 1 \\
2x + y & = e^{3x + 1}
\phantom{000000} [\text{Exponential form}] \\
y & = e^{3x+ 1} - 2x
\end{align}
Use graph to deduce number of solutions
8(i) Sketch the graph of $y = 2 \ln x$ for $x > 0$. Indicate the $x$-intercept of the graph.
Solutions
\begin{align}
y & = 2 \ln x \\
y & = 2 \log_e x \\
\\
\text{Let } & y = 0, \\
0 & = 2 \log_e x \\
0 & = \log_e x \\
e^0 & = x
\phantom{000000} [\text{Exponential form}] \\
1 & = x
\end{align}

8(ii) By adding a straight line to the graph from (i), state the number of solutions to the following equation
$$ x - e^{1 - {1 \over 2}x} = 0 $$
Answer: $ 1 \text{ solution} $
Solutions
\begin{align}
x - e^{1 - {1 \over 2}x} & = 0 \\
x & = e^{1 - {1 \over 2}x} \\
\ln x & = \ln e^{1 - {1 \over 2}x} \\
\ln x & = \left(1 - {1 \over 2}x\right) \ln e
\phantom{000000} [\text{Power law}] \\
\ln x & = \left(1 - {1 \over 2}x\right)(1) \\
\ln x & = 1 - {1 \over 2}x \\
2 \ln x & = 2 \left(1 - {1 \over 2}x\right) \\
2 \ln x & = 2 - x \\
\underbrace{2 \ln x}_\text{Curve} & = \underbrace{-x + 2}_\text{Line} \\
\\
\text{Draw } & y = - x + 2 \\
\\
\text{Let } & x = 0, y = 2 \\
\\
\text{Let } & y = 0, 0 = - x + 2 \\
& \phantom{00000.} x = 2
\\ \\
\text{From sketch, } & \text{equation has only 1 solution}
\end{align}
Real-life problem
9. Students participating in a psychological experiment attended several lectures on a subject. Every month for a year after that, they were tested to see how much of the material they still remembered. The average score, $S$, after $t$ months was given by the model $S = 75 - 6 \ln (t + 1)$, where $0 \le t \le 12$.
(from A Maths 360 2nd edition Ex 5.5)
(i) What was the average score after $4$ months?
Answer: $ 65.3 $
Solutions
\begin{align}
\text{When } & t = 4, \\
S & = 75 - 6\ln [(4) + 1] \\
& = 75 - 6\ln 5 \\
& = 65.343 \\
& = 65.3
\end{align}
(ii) After how many months was the average score about $62$?
Answer: $ 8 $
Solutions
\begin{align}
\text{When } & S = 62, \\
62 & = 75 - 6\ln (t + 1) \\
62 - 75 & = -6 \ln (t + 1) \\
-13 & = -6 \ln (t + 1) \\
{-13 \over -6} & = \ln (t + 1) \\
{13 \over 6} & = \ln (t + 1) \\
{13 \over 6} & = \log_e (t + 1) \\
\\
\implies e^{13 \over 6} & = t + 1 \phantom{0000000000} [\text{Change to exponential form}] \\
\\
t & = e^{13 \over 6} - 1 \\
& = 7.729 \phantom{.} 1 \\
& \approx 8
\end{align}
(iii) Express $t$ in terms of $S$.
Answer: $ t = e^{{1 \over 6}(75 - S)} - 1 $
Solutions
\begin{align}
S & = 75 - 6\ln (t + 1) \\
S - 75 & = -6 \ln (t + 1) \\
75 - S & = 6 \ln (t + 1) \\
{1 \over 6}(75 - S) & = \ln (t + 1) \\
{1 \over 6}(75 - S) & = \log_e (t + 1) \\
\\
e^{{1 \over 6}(75 - S)} & = t + 1 \phantom{0000000000} [\text{Change to exponential form}] \\
\\
t & = e^{{1 \over 6}(75 - S)} - 1
\end{align}
Past year O level questions
| Year & paper |
Comments |
| 2024 P2 Question 3 |
Solve logarithmic equation |
| 2021 P1 Question 12b |
Solve logarithmic equation |
| 4049 Specimen P2 Question 9b, c |
(b) Solve logarithmic equation
Explain why the equation has no real solutions |
| 2020 P2 Question 8b, c |
(b) Solve logarithmic equation
(c) Graph: Use graph to deduce the number of solutions to equation |
| 2019 P2 Question 5a, b |
(a) Solve logarithmic equation
(b) Change subject of equation (take note of part ii) |
| 2018 P1 Question 6 |
Solve logarithmic equation |
| 2017 P2 Question 5 |
Solve logarithmic equation |
| 2017 P2 Question 7b |
Real-life problem |
| 2015 P1 Question 2 |
Graph |
| 2014 Paper 2 Question 5a, b |
(a) Solve logarithmic equation
(b) Change subject of equation |
| 2012 P2 Question 6ai, ii |
(i) Change subject of equation (Link - Subscription required)
(ii) Solve logarithmic equation |
| 2011 P2 Question 5a |
Solve logarithmic equation |
| 2009 P1 Question 4 |
Solve logarithmic equation |
| 2008 P2 Question 4 |
Solve logarithmic equation (part ii involves substitution) |
| 2007 P2 Question 7 |
Solve logarithmic equation |
| 2006 P1 Question 8a, b |
(a) Solve logarithmic equation
(b) Simplify expression (Link - Subscription required) |
| 2005 P1 Question 7a, b |
(a) Solve logarithmic equation
(b) Simplify expression |
| 2004 P2 Question 5 |
Solve logarithmic equation |
| 2003 P2 Question 3 |
Solve logarithmic equation |
| 2002 P1 Question 8ii |
Solve logarithmic equation |
| 2002 P2 Question 8 |
Graph (Link - Subscription required) |
← Exponential functions
Coordinate geometry: Formulas & techniques →