Revision notes
Indices laws for exponential functions
Terms with the same base
$ a^m \times a^n = (a^m)(a^n) = \phantom{.} $ $ a^{m + n} $
$ a^m \div a^n = {a^m \over a^n} = \phantom{.} $ $ a^{m - n} $
Terms with the same power
$ a^m \times b^m = (a^m)(b^m) = \phantom{.} $ $ (ab)^m $
$ a^m \div b^m = {a^m \over b^m} = \phantom{.} $ $ \left(a \over b \right)^m $
Power
$ (a^m)^n = \phantom{.} $ $ a^{mn} $
$ a^0 = \phantom{.} $ $ 1 $
4. Negative indices
$ a^{-n} = \phantom{.} $ $ {1 \over a^n} $
$ {1 \over a^{-n}} = \phantom{.} $ $ a^{-(-n)} = a^n $
$ \left(a \over b\right)^{-n} = \phantom{.} $ $ \left(b \over a\right)^n $
5. Fractional indices
$ a^{1 \over n} = \phantom{.} $ $ \sqrt[n]{a} $
$ a^{1 \over 2} = \phantom{.} $ $ \sqrt{a} $
$ a^{m \over n} = \phantom{.} $ $ \sqrt[n]{a^m} $
How to solve an exponential equation
1. No solution
Equations $3^x = 0$ and $3^x = -3$ have no solutions since $ 3^x > 0 $ for all real values of $x$
2. Solve by changing to the same base on both sides
\begin{align*}
3^x & = 81 \\
3^x & = 3^4 \\
\\
\therefore x & = 4
\end{align*}
3. Solve by taking logarithms (lg or ln) on both sides
\begin{align*}
3^x & = 4 \\
\lg 3^x & = \lg 4 \\
x \lg 3 & = \lg 4
\phantom{000000} [\text{Power law (logarithms)}] \\
x & = {\lg 4 \over \lg 3} \\
x & \approx 1.26
\end{align*}
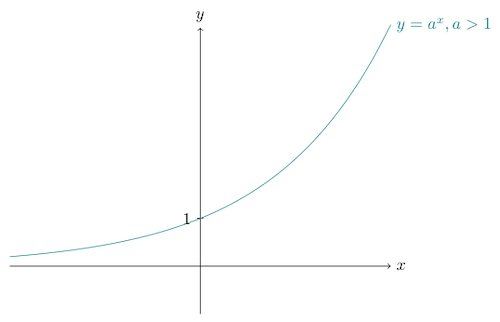
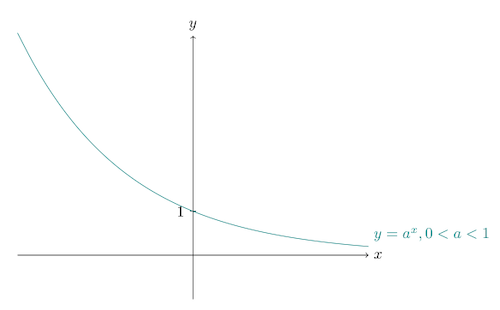
Graph of exponential functions y = ax
1. Graph of $y = a^x$, for $a > 1$
Shape
2. Graph of $y = a^x$, for $0 < a < 1$
Shape
Practice questions
Simplify exponential functions
1. Given that ${9^x \over 3^{x + 1}} = 5^{2 - x}$, find the value of $15^x$.
Answer: $ 75 $
Solutions
\begin{align}
{9^x \over 3^{x + 1}} & = 5^{2 - x} \\
{(3^2)^x \over 3^{x + 1}} & = 5^{2 - x} \\
{3^{2x} \over 3^{x + 1}} & = 5^{2 - x}
\phantom{000000.} [ (a^m)^n = a^{mn}] \\
3^{2x - (x + 1)} & = 5^{2 - x}
\phantom{000000} \left[ {a^m \over a^n} = a^{m - n} \right] \\
3^{x - 1} & = 5^{2 - x} \\
{3^x \over 3^1} & = {5^2 \over 5^x} \\
(3^x)(5^x) & = (3)(5^2) \\
15^x & = 75
\phantom{00000000} [a^m \times b^m = (a \times b)^m]
\end{align}
2. Without using a calculator, simplify the expression ${7^{3x + 1} \times 49^{-1} \over 7^{3x + 1} - 343^x}$.
Answer: $ {1 \over 42} $
(from Think Workbook Worksheet 6A)
Solutions
\begin{align}
\require{cancel}
{ 7^{3x + 1} \times 49^{-1} \over 7^{3x + 1} - 343^x }
& = { 7^{3x + 1} \times (7^2)^{-1} \over 7^{3x + 1} - 7^{3x}} \\
& = { 7^{3x + 1} \times 7^{-2} \over 7^{3x} \times 7 - 7^{3x} } \\
& = { 7^{3x + 1 + (-2)} \over 7^{3x} (7 - 1) }
\phantom{000000} [\text{Factorise}] \\
& = { 7^{3x - 1} \over 7^{3x} (6) } \\
& = { \cancel{7^{3x}} \times 7^{-1} \over \cancel{7^{3x}} (6)} \\
& = { 7^{-1} \over 6 } \\
& = {1 \over 42}
\end{align}
Show that an exponential expression is a multiple of a number
3. Show, for all real values of $n$, that the expression $4^{n + 1} + 3(4^{n + 2}) - 2^{2n + 1}$ is a multiple of $10$.
Solutions
\begin{align}
4^{n + 1} + 3(4^{n + 2}) - 2^{2n + 1} & = 4^n \times 4 + 3(4^n \times 4^2) - 2^{2n} \times 2 \\
& = 4(4^n) + 3[16(4^n)] - 2(2^{2n}) \\
& = 4(4^n) + 48(4^n) - 2[ (2^2)^n] \\
& = 4(4^n) + 48(4^n) - 2(4^n) \\
& = 50(4^n) \\
& = 10[5 (4^n)] \\
\\
\therefore \text{Expression } & \text{is a multiple of } 10
\end{align}
Solve exponential equation
4. Solve the following equations:
(i) $3^{2x + 1} - 3^{2x} = 54$
Answer: $ x = {3 \over 2} $
Solutions
\begin{align}
3^{2x + 1} - 3^{2x} & = 54 \\
(3^{2x})(3) - 3^{2x} & = 54 \\
3^{2x} (3 - 1) & = 54
\phantom{000000} [\text{Factorise } 3^{2x}] \\
3^{2x} (2) & = 54 \\
3^{2x} & = {54 \over 2} \\
3^{2x} & = 27 \\
3^{2x} & = 3^3 \\
\\
2x & = 3 \\
x & = {3 \over 2}
\end{align}
(ii) $4 e^x - 5e^{1 - x} = 0$
Answer: $ x = 0.612 $
Solutions
\begin{align}
4 e^x - 5e^{1 - x} & = 0 \\
4 e^x & = 5 e^{1 - x} \\
{e^x \over e^{1 - x}} & = {5 \over 4} \\
e^{x - (1 - x)} & = {5 \over 4} \\
e^{x - 1 + x} & = {5 \over 4} \\
e^{2x - 1} & = {5 \over 4} \\
\ln e^{2x - 1} & = \ln {5 \over 4} \\
(2x - 1)\ln e & = \ln {5 \over 4}
\phantom{000000} [\text{Power law (logarithms)}] \\
(2x - 1)(1) & = \ln {5 \over 4} \\
2x - 1 & = \ln {5 \over 4} \\
2x & = \ln {5 \over 4} + 1 \\
x & = {1 \over 2} \left( \ln {5 \over 4} + 1 \right) \\
& \approx 0.612
\end{align}
Solve exponential equation by substitution
5. By using a suitable substitution, solve the equation $2^x + 2^{3 - x} = 9$.
Answer: $ x = 0 \text{ or } 3 $
Solutions
\begin{align}
2^x + 2^{3 - x} & = 9 \\
2^x + {2^3 \over 2^x} & = 9 \\
\\
\text{Let } u = 2^x, & \\
u + {8 \over u} & = 9 \\
u \left(u + {8 \over u}\right) & = 9u \\
u^2 + 8 & = 9u \\
u^2 - 9u + 8 & = 0 \\
(u - 1)(u - 8) & = 0
\end{align}
\begin{align}
u - 1 & = 0 && \text{ or } & u - 8 & = 0 \\
u & = 1 &&& u & = 8 \\
\\
2^x & = 1 &&& 2^x & = 8 \\
2^x & = 2^0 &&& 2^x & = 2^3 \\
x & = 0 &&& x & = 3
\end{align}
6. Show that the equation $9^x - 4(3^x) - 5 = 0$ only has one solution.
Solutions
\begin{align}
9^x - 4(3^x) - 5 & = 0 \\
(3^2)^x - 4(3^x) - 5 & = 0 \\
(3^x)^2 - 4(3^x) - 5 & = 0 \\
\\
\text{Let } & u = 3^x, \\
u^2 - 4u - 5 & = 0 \\
(u - 5)(u + 1) & = 0 \\
\\
u - 5 = 0 \phantom{00} & \text{ or } \phantom{00} u + 1 =0 \\
u = 5 \phantom{00} & \phantom{00000000} u = -1 \\
\\
\text{Since } & u = 3^x, \\
3^x = 5 \phantom{0000.} & \text{ or } \phantom{00000} 3^x = -1 \text{ (Reject, since } 3^x > 0) \\
\lg 3^x = \lg 5 \phantom{00.} & \\
x\lg 3 = \lg 5 \phantom{00.} & \\
x = {\lg 5 \over \lg 3} \phantom{0(} & \\
x = 1.4549 & \\
x \approx 1.45 \phantom{00} & \\
\\ \\
\therefore x = 1.45 & \text{ is the only solution}
\end{align}
Solve simultaneous equations
7. Solve the following simultaneous equations:
$$ { 9^{2x} \over 81^{y - 1} } = 27 \text{ and } 4^{3y} \times 8 = 32^x $$
(from Thinks A Maths Workbook Worksheet 6A)
Answer: $ x = -{9 \over 2}, y = -{17 \over 4} $
Solutions
\begin{align}
{9^{2x} \over 81^{y - 1}} & = 27 \\
{(3^2)^{2x} \over (3^4)^{y - 1}} & = 3^3 \\
{3^{4x} \over 3^{4y - 4} } & = 3^3 \\
3^{4x - (4y - 4)} & = 3^3 \\
\\
4x - (4y - 4) & = 3 \\
4x - 4y + 4 & = 3 \\
4x - 4y & = -1 \phantom{00} \text{--- (1)} \\
\\ \\
4^{3y} \times 8 & = 32^x \\
(2^2)^{3y} \times 2^3 & = (2^5)^x \\
2^{6y} \times 2^3 & = 2^{5x} \\
2^{6y + 3} & = 2^{5x} \\
\\
6y + 3 & = 5x \\
6y & = 5x - 3 \\
y & = {1 \over 6}(5x - 3) \\
y & = {5 \over 6}x - {1 \over 2} \phantom{00} \text{--- (2)} \\
\\ \\
\text{Substitute } & \text{(2) into (1),} \\
4x - 4\left({5 \over 6}x - {1 \over 2}\right) & = -1 \\
4x - {10 \over 3}x + 2 & = -1 \\
{2 \over 3}x & = -3 \\
x & = -3 \div {2 \over 3} \\
x & = -{9 \over 2} \\
\\
\text{Substitute } & \text{into (2),} \\
y & = {5 \over 6} \left(-{9 \over 2}\right) - {1 \over 2} \\
y & = -{17 \over 4} \\
\\ \\
\therefore x & = -{9 \over 2}, y = -{17 \over 4}
\end{align}
Graphs of exponential functions
Sketch exponential graphs and find the number of solutions
8(i) Sketch the graph of $y = 2.5^x$.
(from A Maths 360 2nd Edition Ex 5.2
Solutions
\begin{align}
\text{When } & x = 0, \\
y & = 2.5^0) \\
& = 1 \\
\\
\implies & y \text{-intercept is } 1
\end{align}
8(ii) By adding a straight line to the sketch in (i), state the number of solutions to the equation $2.5^x + x = 6$.
Answer: $ 1 \text{ solution} $
Solutions
\begin{align}
2.5^x + x & = 6 \\
\underbrace{2.5^x}_{\text{Curve }} & = \underbrace{6 - x}_{\text{Line}} \\
\\
\text{Draw } & y = 6 - x \\
\\
\text{Let } & x = 0, y = 6 \\
\\
\text{Let } & y = 0, x = 6 \\
\\
\\
\text{From sketch, } & \text{there is only 1 solution}
\end{align}
Find the values of constants in an exponential equation
9. The curve $y = ae^{bx}$ passes through the points $(0.5, 1.1)$ and $(1.5, 0.15)$. Find, correct to 3 significant figures, the value of $a$ and of $b$.
(from A Maths 360 2nd Edition Revision Ex 5)
Answer: $ a \approx 2.98, b \approx -1.99 $
Solutions
\begin{align}
y & = ae^{bx} \\
\\
\text{Using } (0.5 , 1.1), & \text{ when } x = 0.5, y = 1.1, \\
1.1 & = ae^{b(0.5)} \\
1.1 & = ae^{0.5b} \phantom{000} \text{--- (1)} \\
\\
\text{Using } (1.5, 0.15), & \text{ when } x = 1.5, y = 0.15, \\
0.15 & = ae^{b(1.5)} \\
0.15 & = ae^{1.5b} \phantom{000} \text{--- (2)} \\
\\
(2) & \div (1), \\
{0.15 \over 1.1} & = {ae^{1.5b} \over ae^{0.5b}} \\
{3 \over 22} & = {e^{1.5b} \over e^{0.5b}} \\
{3 \over 22} & = e^{1.5b - 0.5b} \\
{3 \over 22} & = e^b \\
\\
\text{Taking } \ln & \text{ of both sides,} \\
\ln {3 \over 22} & = \ln e^b \\
\ln {3 \over 22} & = b \ln e \\
\ln {3 \over 22} & = b (1) \\
\ln {3 \over 22} & = b \\
\\
\text{Substitute } & b = \ln {3 \over 22} \text{ into (1),} \\
1.1 & = ae^{0.5 \ln {3 \over 22}} \\
1.1 & = a(0.36927) \\
{1.1 \over 0.36927} & = a \\
2.9788 & = a \\
2.98 & \approx a \\
\\
\therefore a & \approx 2.98, b = \ln {3 \over 22} = -1.9924 \approx -1.99
\end{align}
Exponential functions in real-world context
10. The population, $P$, of fish in a lake $t$ months after a nearby chemical factory commenced operation is given by $P = 600(2 + e^{-0.2t})$.
(from A Maths 360 2nd Edition Ex 5.2)
Find the number of fish in the lake
(i) just before the factory started operation,
Answer: $ 1 \phantom{.} 800 $
Solutions
\begin{align}
\text{When } & t = 0, \\
P & = 600(2 + e^{-0.2(0)}) \\
& = 600(2 + 1) \\
& = 1 \phantom{.} 800
\end{align}
(ii) after 1 year,
Answer: $ 1 \phantom{.} 254 $
Solutions
\begin{align}
\text{When } & t = 12, \\
P & = 600(2 + e^{-0.2(12)}) \\
& = 1 \phantom{.} 254.430 \phantom{.} 77 \\
& \approx 1 \phantom{.} 254
\end{align}
(iii) in the long run.
Answer: $ 1 \phantom{.} 200 $
Solutions
\begin{align}
P & = 600(2 + e^{-0.2t}) \\
& = 600\left( 2 + {1 \over e^{0.2t}} \right)
\end{align}
\begin{align}
\text{As } t \rightarrow \infty &, \phantom{0} {1 \over e^{0.2t}} \rightarrow 0 \\
\\
\therefore P & = 600(2 + 0) \\
& = 1 \phantom{.} 200
\end{align}
Form exponential equation using information provided
11. The initial value of an investment is $ \$ 10 \phantom{.} 000$ and it increases by 5% every year.
(i) Show that the value of the investment, $V$, after $n$ years is $ \$ 10 \phantom{.} 000 (1.05)^n $
Solutions
\begin{align}
\text{Value after 1 year, } V & = 10 \phantom{.} 000 \times {105 \over 100}
\phantom{000000} [100\% + 5\% = 105\%] \\
& = 10 \phantom{.} 000 (1.05) \\
\\
\text{Value after 2 years, } V & = 10 \phantom{.} 000 (1.05) \times {105 \over 100}
\phantom{000000} [105\% \text{ of the amount from year 1}] \\
& = 10 \phantom{.} 000 (1.05)^2 \\
\\
\text{Value after 3 years, } V & = 10 \phantom{.} 000 (1.05)^2 \times {105 \over 100}
\phantom{000000} [105\% \text{ of the amount from year 2}] \\
& = 10 \phantom{.} 000 (1.05)^3 \\
& . \\
& . \\
& . \\
\text{Value after } n \text{ years, } V & = 10 \phantom{.} 000 (1.05)^n \phantom{00} (\text{Shown})
\end{align}
(ii) Find the number of years required for the investment to triple in value.
Answer: $ 23 $
Solutions
\begin{align}
\text{Initial value} & = \$10 \phantom{.} 000 \\
\\
\text{Triple of initial value} & = \$ 30 \phantom{.} 000 \\
\\
\text{Let } & V = 30 \phantom{.} 000, \\
30 \phantom{.} 000 & = 10 \phantom{.} 000 (1.05)^n \\
{30 \phantom{.} 000 \over 10 \phantom{.} 000} & = (1.05)^n \\
3 & = (1.05)^n \\
\lg 3 & = \lg (1.05)^n \\
\lg 3 & = n \lg 1.05
\phantom{000000} [\text{Power law (logarithms)}] \\
{\lg 3 \over \lg 1.05} & = n \\
22.517 & = n \\
\\
\text{Number of years} & = 23
\end{align}
O Level past year questions on exponential functions
Fully worked, step-by-step solutions to these past-year questions (2016 to 2025) are in the O Level A Maths Solutions page. For 2015 and earlier, selected questions and their solutions are available to subscribers, linked individually in the table below.
| Year & paper |
Comments |
| 2025 P1 Question 1 |
Real-life problem: Form equation |
| 2025 P2 Question 8 |
(a) Solve exponential equation (b) Solve simultaneous equations (Tedious) |
| 2024 P2 Question 1 |
Real-life problem |
| 2024 P2 Question 5b |
Solve exponential equation by substitution |
| 2023 P2 Question 3 |
Real-life problem |
| 2023 P2 Question 6b |
Solve exponential equation by substitution |
| 2022 P2 Question 1 |
Real-life problem |
| 2022 P2 Question 6a |
Solve exponential equation by substitution |
| 2022 P2 Question 6bi |
Graph: Find x and y intercepts of curve |
| 2021 P1 Question 12a |
Solve exponential equation |
| 2021 P2 Question 1 |
Solve exponential equation by substitution |
| 4049 Specimen P1 Question 5 |
Real-life problem |
| 4049 Specimen P2 Question 9a |
Solve exponential equation by substitution |
| 2020 P1 Question 2a |
Simplify exponential expression |
| 2020 P1 Question 2b |
Real-life problem |
| 2020 P2 Question 8a |
Solve exponential equation by substitution |
| 2019 P1 Question 5 |
Real-life problem (take note of part i) |
| 2019 P1 Question 10a |
Solve simultaneous equations |
| 2018 P1 Question 1 |
Solve exponential equation |
| 2017 P2 Question 7a |
Real-life problem |
| 2016 P2 Question 7 |
Solve exponential equation by substitution |
| 2015 P1 Question 3 |
Real-life problem |
| 2014 P2 Question 1 |
Real-life problem |
| 2013 P1 Question 8 |
Real-life problem (take note of part iv) |
| 2013 P2 Question 8b |
Solve exponential equation by substitution |
| 2012 P1 Question 12i |
Solve exponential equation |
| 2012 P2 Question 6b |
Solve exponential equation by substitution |
| 2011 P1 Question 3 |
Solve exponential equation (Link 🔒 Subscribers) |
| 2011 P2 Question 5b |
Graph (Link 🔒 Subscribers) |
| 2010 P2 Question 3 |
Solve simultaneous equations |
| 2010 P2 Question 5 |
Graph (Link 🔒 Subscribers) |
| 2009 P2 Question 3 |
Solve exponential equation by substitution (form cubic equation) |
| 2008 P1 Question 2 |
Solve simultaneous equations |
| 2008 P2 Question 1 |
Real-life problem |
| 2007 P1 Question 3 |
Real-life problem (Link 🔒 Subscribers) |
| 2006 P2 Question 9b |
Simplify expression (Link 🔒 Subscribers) |
| 2005 P2 Question 1 |
Solve exponential equation |
| 2005 P2 Question 8a |
Simplify expression (Link 🔒 Subscribers) |
| 2005 P2 Question 8b |
Solve exponential equation by substitution |
| 2004 P1 Question 3 |
Solve simultaneous equations |
| 2004 P1 Question 12 Either |
(a) Real-life problem (b) Solve exponential equation |
| 2003 P1 Question 2 |
Solve exponential equation |
| 2002 P1 Question 8i |
Solve exponential equation by substitution |
| 2002 P2 Question 9a |
Simplify expression |
| 2002 P2 Question 9b |
Solve exponential equation (Link 🔒 Subscribers) |
← Binomial theorem: General term
Logarithms →
