Plane geometry
Angle properties
Angle between two intersecting lines:
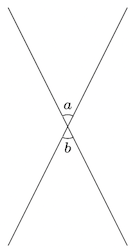
$ \angle a = \angle b \phantom{0} ($ $ \text{Vertically opposite angles} $ $\text{)}$
Angle bisector:

$ \text{If } DB \text{ bisects } \angle ABC, \text{ then }$ $ \angle ABD = \angle CBD $
Parallel lines:
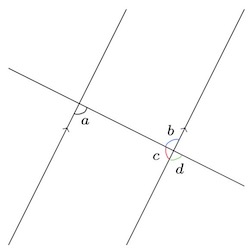
$ \angle a = \angle b \phantom{0} ($ $ \text{Alternate angles} $ $\text{)}$
$ \angle a + \angle c = $ $ 180^\circ \text{ (Interior angles} $$\text{)}$
$ \angle a = \angle d \phantom{0} ($ $ \text{Corresponding angles} $ $\text{)}$
Common angle:

$ \angle BAC = $ $ \angle CAD $ $ \text{ (Common angle)}$
Midpoint theorem
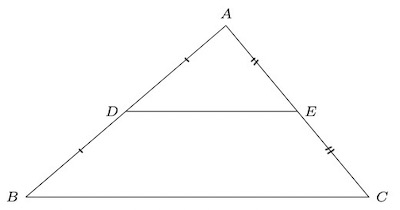
If D is the midpoint of AB and E is the midpoint of AC, then
$ DE \phantom{.} // \phantom{.} BC $ $\text{ and } $ $ DE = {1 \over 2} BC $
Circle properties
Properties from E maths:
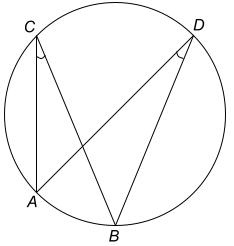
$ \angle ACB = \angle ADB \text{ (}$ $ \text{Angles in the same segment} $ $ \text{)} $
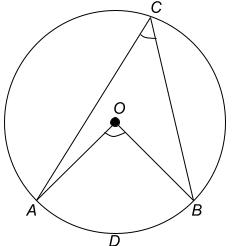
If O is the centre of the circle,
$ \angle AOB = 2 \times \angle ACB \text{ (}$ $ \text{Angle at centre} = 2 \times \text{Angle at circumference} $ $ \text{)} $
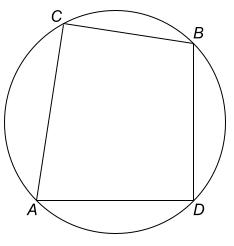
$ \angle ACB + \angle ADB = 180^\circ \text{ (}$ $ \text{Angles in opposite segments} $ $ \text{)} $
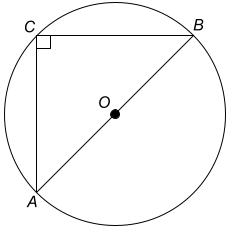
If AOB is the diameter of the circle,
$ \angle ACB = 90^\circ \text{ (}$ $ \text{Right-angle in semi-circle} $ $ \text{)} $
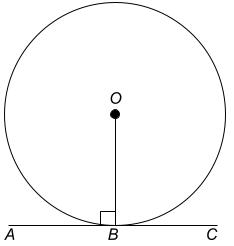
If O is the centre of the circle and the line AC is tangent to the circle at B,
$ \angle OBA = 90^\circ \text{ (}$ $ \text{Tangent perpendicular to radius} $ $ \text{)} $
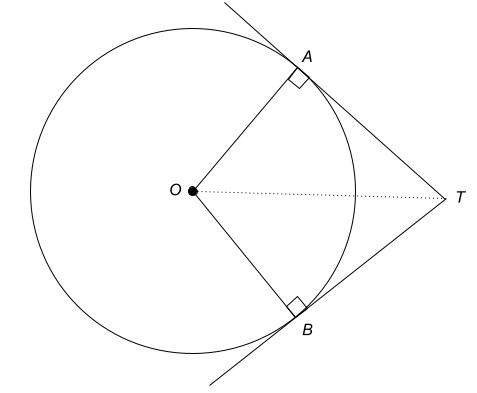
If O is the centre of the circle and tangents to the circle at A and at B meet at an external point T, then
$ AT = BT $ $ \text{ and } $ $ \angle OTA = \angle OTB $
Alternate segment theorem (or tangent-chord theorem):
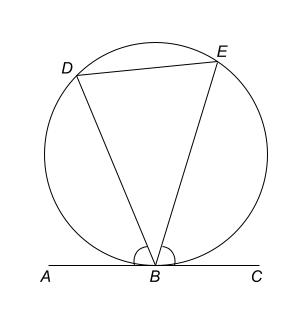
If the line AC is tangent to the circle at B,
$ \angle DBA = $$ \angle DEB $ $ \text{ (Alternate segment theorem)} $
$ \angle EBC = $$ \angle EDB $ $ \text{ (Alternate segment theorem)} $
Proving questions
Congruency tests for triangles:
- Side-Side-Side (SSS)
- Angle-Side-Angle (ASA)
- Angle-Angle-Side (AAS)
- Right angle-Hypotenuse-Side (RHS)
- Side-Angle-Side (SAS)
Similarity tests for triangles:
- Side-Side-Side (SSS)
- Angle-angle (AA)
- Side-Angle-Side (SAS)
Examples

1. In the diagram, $AB$ is a diameter of the circle with centre $O$. Chords $AD$ and $BC$ intersect at $P$. $\angle POB = 90^\circ$. The tangent to the circle at $B$ meets $AD$ produced at $Q$. $AQ$ bisects $ \angle CAB$.
(from think! Workbook Worksheet 17C)
(i) Show that $ DB $ bisects $\angle PBQ$.
(ii) Show that triangles $AOP$ and $ADB$ are similar.
(iii) Show that $ AO^2 = {1 \over 2} \times AP \times AD $.

2. The diagram shows a circle passing through $A$, $B$, $C$ and $D$. The tangent to the circle at $A$ and $CB$ produced intersect at the point $P$. $DA$ is parallel to $CB$ and $DA = DC$.
(from think! Workbook Specimen Paper B)
(i) Show that triangle $PAB$ is isosceles.
(ii) Show that $AP$ and $DB$ are parallel.
Past year O level questions
| Year & paper | Comments |
|---|---|
| 2025 P2 Question 10 | [Part (b)(ii) is difficult] |
| 2024 P1 Question 6 | |
| 2023 P2 Question 2 | (b) Deduce the type of quadrilateral formed |
| 2022 P1 Question 7 | (ii) Prove isosceles triangle |
| 2021 P1 Question 11 | (a) Prove isosceles triangle |
| 2020 P2 Question 4 | Prove that two lines are parallel |
| 2019 P1 Question 6 | |
| 2018 P2 Question 3 | Prove that line bisects angle |
| 2017 P1 Question 10 | (ii) Prove equation |
| 2016 P2 Question 5 | (ii) Prove that two lines are parallel |
| 2015 P1 Question 9 | (ii) Prove isosceles triangle |
| 2014 P2 Question 6 | Prove various equations |
| 2013 P2 Question 2 | Prove isosceles triangle (Link - Subscription required) |
| 2012 P2 Question 4 | (ii) Prove equation (Link - Subscription required) |
| 2011 P2 Question 7 | (ii) Prove equation (Link - Subscription required) |
| 2010 P2 Question 6 | (i) Prove isosceles triangle (ii) Prove line bisects angle (iii) Prove similar triangle |
| 2009 P2 Question 4 | Prove isosceles triangle (need to use congruent triangles) (Link - Subscription required) |
| 2008 P2 Question 6 | Prove that E is the midpoint of AD (need to use similar triangles & congruent triangles) (Link - Subscription required) |