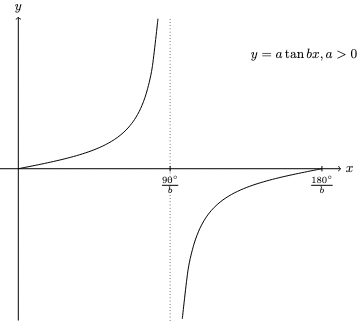
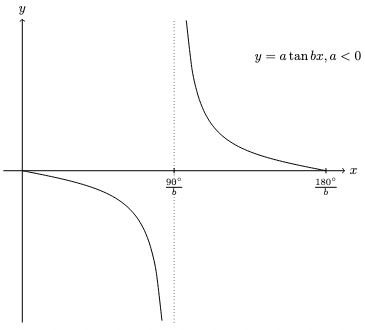
Tangent graph
Shape and features of graph
$$ \text{General equation: } y = a \tan bx $$
Questions
Deduce equation from graph
1. The diagram below shows the graph of $y = \tan ax$.

Determine the value of $a$.
Answer: $ a = {3 \over 2} $
Sketch question
2. Sketch the graph of $y = - \tan 2x$, for $0^\circ \le x \le 360^\circ$.
Past year O level question: 2011 P2 Question 2
(Note: This is the only question on tangent graph - from 2002 to 2025)
3. The function $f$ is given by $f(x) = a \tan bx$, where $a$ and $b$ are positive integers and $ -{\pi \over 2} \le x \le {\pi \over 2}$.
(i) Given that $f(x) = 0$ when $x = {\pi \over 2}$, find the smallest possible value of $b$.
[1]
Answer: $ b = 2 $
(ii) Using the value of $b$ found in part (i) and given that the gradient of the graph of $y = f(x)$ is $12$ at the point where $x = {\pi \over 8}$, find the value of $a$.
(Note: This part is about differentiation)
[3]
Answer: $ a = 3 $
(iii) Sketch the graph of $y = f(x)$.
[3]
← Trigonometry: Cosine graph Trigonometry: Find trigonometric ratio without calculator →